Deformation of materials can be defined as macroscopic changes to the size and shape of materials under the effect of mechanical loading, thermal loading or phase transformation, etc. From a mechanical point of view, it is possible to classify deformation into two as elastic and plastic deformation.
Elastic & Plastic Deformation
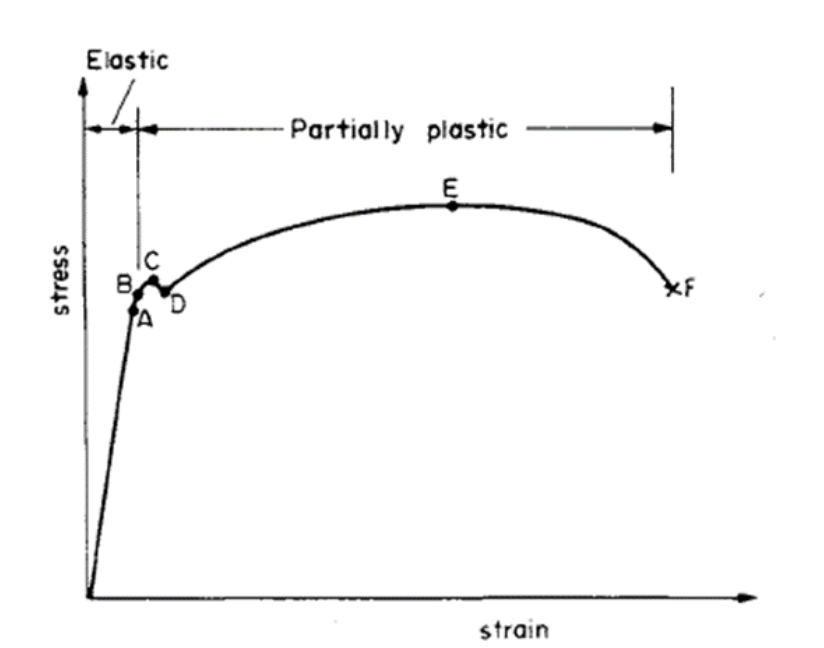
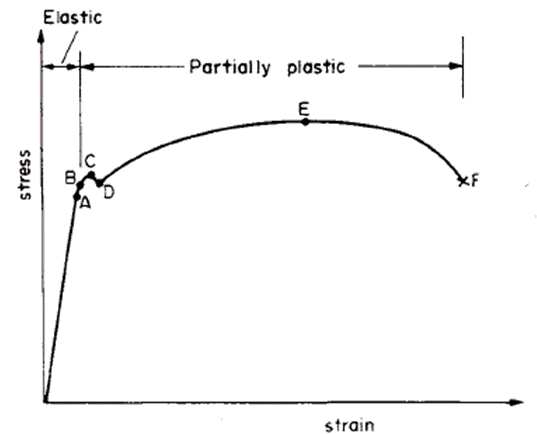
When the external stress does not exceed the yield strength of the material, the material undergoes elastic deformation, which is nonpermanent, meaning, as the applied stress is removed, the material tends to turn back to its original size and shape. In the elastic region, stress and strain increase proportionally to each other by perfectly following Hook’s Law. As the applied stress increases above the yield point, the plastic deformation stage initiates in which, the material deforms much quicker, and permanently. Within the plastic region there are both elastic and plastic deformation exist. Figure 1 represents a typical stress-strain diagram of a metal. Here, point A represent proportionality limit at which linear nature of the graph disappears, and point B represents yield strength (elasticity limit) of the material. Beyond point B is called as plastic region in which, strain is permanent. During plastic deformation, some cracks are formed and propagate until the material fractures completely.
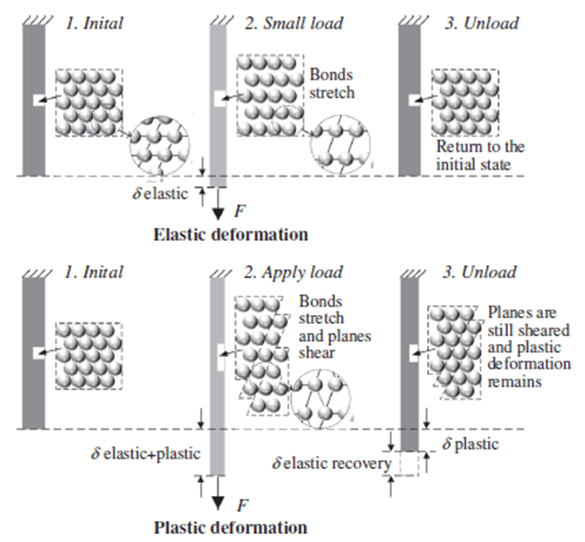
The fundamental mechanism that plastic deformation relies on is the movement of dislocations. In the elastic region, since applied stress is lower than the yield point it cannot activate dislocation movement, so atomic bonds only stretch temporarily and return to their original state when stress is removed. However, within the plastic region, the applied stress exceeds the yield point so, it can activate deformation movement. Here, atomic bonds both stretch and break, and planes shear over each other, thereby material deforms permanently. Figure 2 represents differences between elastic and plastic deformation in atomic scale. As can be seen from the figure, during plastic deformation, after the load is removed, while shear planes have remained, stretched bonds are recovered.
Role of Dislocations in Plastic Deformation
Dislocations are defects where an extra half plane is inserted into the lattice. There are mainly two types of dislocations as edge and screw, sometimes they both appear at the same time which is then called mixed dislocation. In general, there are two types of dislocation movement as glide and climb. During glide, dislocations move along a surface defined by their burgers vector; on the other hand, during climb, dislocations move outward the glide surface. Plastic deformation in metals develops by predominantly shearing, which means sliding of lattice planes over each other by allowing macroscopic changes without affecting atomic arrangement. Stress that is required for plastic deformation can be lowered by localizing deformation by line defect movement instead of sliding the entire lattice plane. While required force to break the entire atomic bonds at a time is great, by moving dislocations along planes allows atoms to slip over each other at a lower stress. Therefore, the principal mechanism of plastic deformation in metals is the generation and movement of dislocations.
Plastic Deformation Mechanisms
In many metals, the basic mechanism of plastic deformation is slip movement. However, in cases where slip is not possible, twinning becomes the basis of plastic deformation. Besides slip and twinning in single crystals, there are also more complicated deformation mechanisms exist that are responsible for plastic deformation in polycrystalline metals as grain boundary sliding.
Slip
Slip is a movement of atoms’ slipping over each other within crystal lattice when the applied stress exceeds the critical resolved shear stress of the material. Slip occurs via the movement of dislocations along close-packed planes and directions, which contains most atoms per unit length. The term slip system represents the set of slip planes and directions in which the dislocation movement requires fewer amounts of energy. There is a remarkable increase in theoretically calculated resolved shear stress when compared to experimental results due to the existence of dislocations. Instead of generating new dislocations, by making an existing one to move along the slip plane, it is possible to promote plastic deformation via slip. Commonly slip is the fundamental mechanism of plastic deformation if only the structure is consists of close-packed slip systems at enough amount, otherwise, other deformation mechanisms step in.
Twinning
Although generally, plastic deformation realizes via slip movement, in some cases in which fewer slip systems exist, twinning becomes the fundamental mechanism of deformation. Twinning is the rearrangement process of atoms subjected to deformation, which results in a change in orientation of atoms thus, local atoms rearrange as mirror images of each other across a twinning plane. Similar to slip, twinning realizes across definite crystallographic planes, and directions called twin plane and twin directions. During twinning, atoms parallel to the twin plane, move along the lattice by leading distortion in lattice within the twinned region. The amount of movement is directly proportional to the distance of each atomic plane to the twin plane. Twinning contributes to plastic deformation by allowing planes to develop further slip by endamaging the plane orientation.
Grain Boundary Sliding
Grain boundary sliding is a grain-size sensitive deformation mechanism that allows grains to slide through each other by changing grain shape via shear deformation along the boundaries without causing any friction or void formation. Since the mechanism occurs via diffusive mass transfer, it is linked with superplasticity development. In high temperature and low stress, deformation is developed via mutual accommodation of both grain boundary sliding and mass transfer. For the diffusive mass transfer, the strain in grain shapes is accommodated by diffusion creep, which is also grain-size sensitive and occurs at high temperature and low strain rate. Therefore, high temperature is a must to provide for grain boundary sliding to occur. In such conditions, the strain is produced by neighbor switching, which results in a large amount of deformation without remarkable internal deformation of grains. This process is called superplastic deformation.
Plastic Deformation Ability of a Metal
To determine whether the material can undergo plastic deformation or not, besides process variables as applied stress, temperature, etc., the mechanical properties of the material constitute a great significance. As it has mentioned before, for material to deform plastically, atomic bonds should not only be extended but also be broken which, can only be possible when the applied stress exceeds the yield strength of the material. Therefore, as the yield strength of a material increases, it gets more challenging to deform it plastically. As a reversely proportional property to yield strength, ductility represents the ability of a material to undergo deformation without fracturing or cracking. By performing a tensile test, it is possible to observe measures of ductility as elongation at fracture and reduction in area that the material exhibits. Even by just visual investigation of a stress-strain diagram after a tensile test, ductility can be identified: materials having a wider curve on the diagram are considered as ductile. Any factors having a reductive effect on ductility would also affect the deformation ability of material in the same manner, such as strength and hardness.
References
[1]https://www.sciencedirect.com/science/article/pii/B978044453770600017
[2]https://www.sciencedirect.com/science/article/pii/B978012814381000001
[3]https://www.sciencedirect.com/science/article/pii/B978075063265250002
[4] https://engineeringlibrary.org/reference/properties-of-metals-doe-handbook
[5]https://www.sciencedirect.com/science/article/pii/B978075068287900006
[6]https://www.researchgate.net/publication/27345883_Modelling_plastic_deformation_of_metals_using_irreversible_thermodynamics/figures?lo=1